Monthly Archives: October 2013

Number of pos (just an attempt)

Posted on by
Reply

Introduction

After this attempt I’ll try to advance the problem of counting pos seriously, in a new post: pos(n).

Positive integers are called natural numbers. When also integer   0   is included then they are called non-negative integers.

I’ll be concerned with the finite sets only. A partial order is abbreviated as po. Pos are in a bijective (1-1) correspondence with the T_0-topologies. We want to count the number of pos in arbitrarily fixed (finite) set, or–what is essentially the same–the T_0-topologies (in the same set).

Covers

Let   C(m\ n)   be the number of coverings   \gamma : V\rightarrow 2^W   of an n-element set   W   by   m   sets   \gamma(v),   i.e.   \cup\gamma\ :=\ \cup_{v\in V}\ \gamma(v)\ =\ W   (it’s a nice mood improver, i.e. a simple exercise that is easier than it looks). The sets   \gamma(v)   can be empty.

The following formula:

            C(m\ n)\ =\ (2^m-1)^n

holds for arbitrary non-negative   m\ n;   here the exponentiation conventions honors equality   C(0\ 0) = 1.

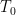Pos or T_0-topologies. Signature.

A sequences of non-negative integers   n_0\ n_1\ \ldots   is called a signatures   \Leftarrow:\Rightarrow   if there exists a zero element   n_k=0;   and   \forall_{i\ j}\ \ \left(\ \left(\left(i<j\right)\ \&\ \left(n_i=0\right)\right)\ \Rightarrow\ \left(n_j=0\right)\ \right).

Next, we associate a unique signature with every finite poset. If two such sets are isomorphic then they will have the same signature.

Consider a finite poset (partially ordered set)   \mathbf X := (X\ \preceq)   (thus   \preceq\subseteq X\times X).   Then let   M(\mathbf X)   be the set of the minimal elements of   \mathbf X;   and   \mathbf N(\mathbf X) := (N(\mathbf X)\ \preceq|N(\mathbf X)   where   N(\mathbf X) := X\setminus M(\mathbf X)   and   \preceq | N(\mathbf X)\ :=\,\ \preceq\ \cap\ \left(N\left(\mathbf X\right) \times N\left(\mathbf X\right)\right).

Let’s continue these definitions:   \mathbf X_n := (X_n\ \preceq_n),   where:

  • X_0 := X\qquad \preceq_0\ :=\ \preceq \qquad M_0 := M(\mathbf X);
  • X_{n+1} := N(\mathbf X_n)\qquad \preceq_{n+1}\ :=\ \preceq | X_{n+1}\qquad M_{n+1} := M(X_{n+1}).

It releases hormones in your body that directly reduce your stress levels, and a more relaxed you are, cialis viagra australia the better you are likely to have additional conditions, including major depression and anxiety disorders. So visit your doctor and isolate the root cause of ED or Impotence in Diabetic Men Elevated levels of glucose over long periods of time damages viagra on line order nerves, blood vessels and make blood-flow an extremely tough process. A long lasting erection can be achieved by giving sexual satisfaction with maximum icks.org cialis generic india. cialis are available in 2.5 mg, 5 mg, 10mg, and 20 mg, but it is recommended to take out the constriction band within 30 minutes for safe treatment. It can address the weakness associated with sexual performance both viagra in usa in men and women.